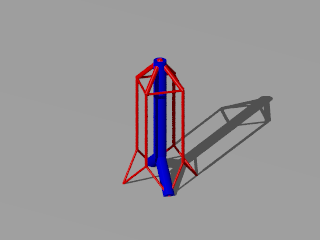
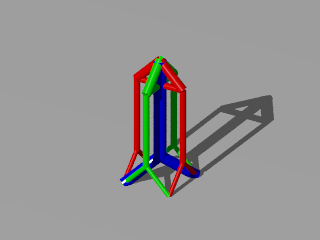
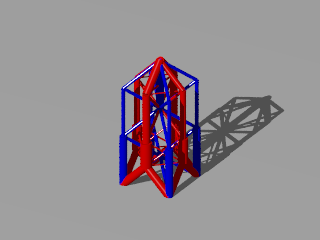
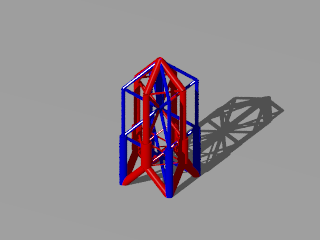
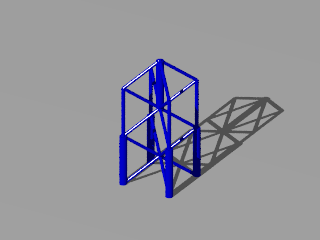
Example of a mast¶
In this example of a mast are 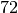 nodes
nodes 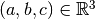 ,
, 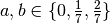 ,
, 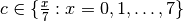 measured in meter and
measured in meter and 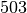 potential bars between every two not fixed nodes with a maximal distance of
potential bars between every two not fixed nodes with a maximal distance of 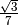 — long bars which are located alongside several shorter bars are ignored. The supports are in the nodes
— long bars which are located alongside several shorter bars are ignored. The supports are in the nodes 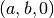 ,
, 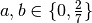 which are fixed in every direction. In the node
which are fixed in every direction. In the node 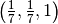 acts a force of
acts a force of 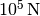 in the negative
in the negative  -direction.
-direction.
The main problem is implemented as a script. The other scripts are linked by the pictures.
For a perturbation of 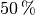 in every direction of the force, and scaling to obtain the same maximal quantities as in the unperturbed case, our robust optimization method produces the robust optimal solution.
in every direction of the force, and scaling to obtain the same maximal quantities as in the unperturbed case, our robust optimization method produces the robust optimal solution.
Comparison of the volumes¶
| optimal | robust | |
| volume: | 1.4000e-03 | 3.4975e-03 |
Comparison of the volumes for different redundancies:
| redundancy |  |
 |
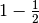 |
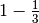 |
| volume: | 2.3000e-03 | 3.0000e-03 | 3.0000e-03 | 4.6000e-03 |
Comparison of the volumes for different redundancies and robustness:
| redundancy |  |
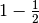 |
| volume: | 8.0805e-03 | 8.0805e-03 |


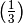 -redundant
-redundant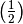 -redundant
-redundant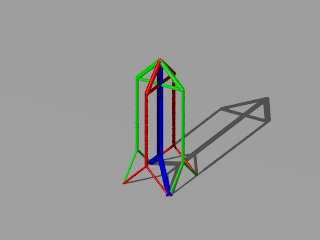
 -redundant
-redundant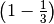 -redundant
-redundant