Example 3¶
This is a 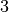 -dimensional example with the ground structure of
-dimensional example with the ground structure of 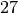 nodes
nodes 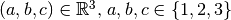 measured in meter and
measured in meter and 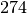 potential bars between every two not fixed nodes – long bars which are located alongside several shorter bars are ignored. The supports are in the nodes
potential bars between every two not fixed nodes – long bars which are located alongside several shorter bars are ignored. The supports are in the nodes 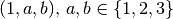 which are fixed in every direction. In the node
which are fixed in every direction. In the node 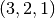 acts a force of
acts a force of 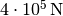 in the negative
in the negative  -direction.
-direction.
For a perturbation of 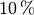 in every direction of the force, and scaling to obtain the same maximal quantities as in the unperturbed case, our robust optimization method produces the robust optimal solutions. In contrast to the optimal solution the robust solution use the third dimension of the space.
in every direction of the force, and scaling to obtain the same maximal quantities as in the unperturbed case, our robust optimization method produces the robust optimal solutions. In contrast to the optimal solution the robust solution use the third dimension of the space.
Comparison of the volumes¶
| optimal | robust | |
| volume: | 6.0000e-03 | 6.5822e-03 |
Comparison of the volumes for different redundancies:
| redundancy |  |
 |
 |
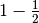 |
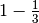 |
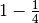 |
| volume: | 8.6667e-03 | 9.5000e-03 | 1.2000e-02 | 1.2000e-02 | 1.9000e-02 | 2.6000e-02 |
Comparison of the volumes for different redundancies and robustness:
| redundancy |  |
 |
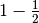 |
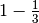 |
| volume: | 1.2136e-02 | 1.5528e-02 | 1.5528e-02 | 2.4875e-02 |
Visualizations¶
Optimal solutions: (script)

|
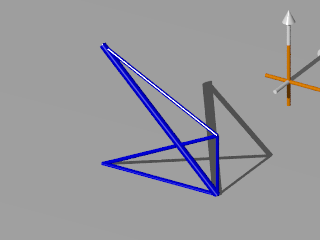
|
Robust solutions: (script)
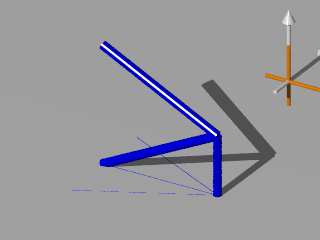
|
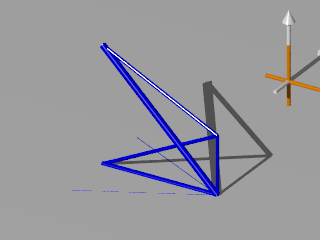
|
Redundant solutions: (script)
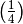 -redundant -redundant |
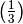 -redundant -redundant |

|

|
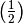 -redundant -redundant |
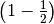 -redundant -redundant |
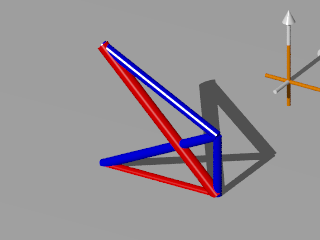
|
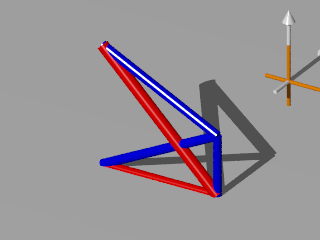
|
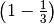 -redundant -redundant |
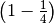 -redundant -redundant |

|

|
Robust and redundant solutions:
robust and 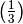 -redundant: (script) -redundant: (script) |
robust and 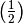 -redundant: (script) -redundant: (script) |
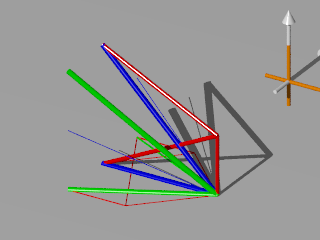
|
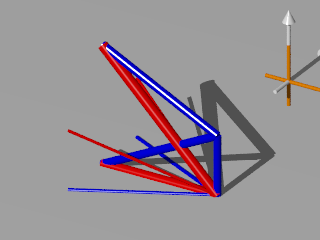
|
robust and 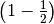 -redundant: (script) -redundant: (script) |
robust and 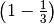 -redundant: (script) -redundant: (script) |
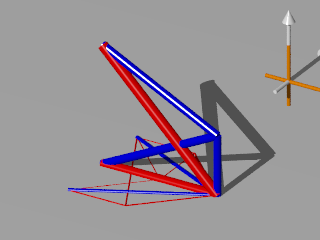
|
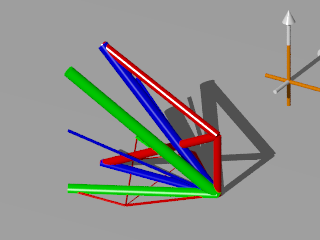
|
